Hướng dẫn này sẽ dạy bạn cách viết chương trình python để kiểm tra xem một số có phải là số nguyên tố hay không.
Nếu bạn đã từng làm bài kiểm tra mã hóa, bạn đã bắt gặp một câu hỏi toán học trong bài kiểm tra số nguyên tố hoặc số nguyên tố. Trong vài phút tới, bạn sẽ học cách đưa ra giải pháp tối ưu cho câu hỏi này.
Trong hướng dẫn này:
- tìm hiểu những điều cơ bản của số nguyên tố,
- viết mã python để kiểm tra xem một số có phải là số nguyên tố không và
- tối ưu hóa nó hơn nữa để có được thuật toán thời gian chạy O(√n).
Đối với tất cả những điều này và hơn thế nữa, hãy bắt đầu.
Một số nguyên tố là gì?
Hãy bắt đầu bằng cách làm quen với những điều cơ bản về số nguyên tố.
Trong lý thuyết số, một số tự nhiên n được gọi là số nguyên tố nếu nó có đúng hai ước: 1 và cùng một số (n). Nhớ lại bài toán ở trường: số i được gọi là ước của n nếu i chia n đều.
Bảng sau đây liệt kê một số số, tất cả các thừa số của chúng và số nguyên tố.
nFactorsCó phải là số một không? 11Không21, 2Có31, 3Có41, 24No71, 7Yes151, 3, 515Không
Từ bảng trên, chúng ta có thể viết:
- 2 là số nguyên tố nhỏ nhất.
- 1 là một thừa số của mọi số.
- Mỗi số n là một yếu tố trong chính nó.
Như vậy 1 và in là các thừa số tầm thường cho mọi số n. Và một số nguyên tố không được có thừa số nào khác ngoài hai thừa số này.
Điều này có nghĩa là khi bạn đi từ 2 đến n- 1bạn sẽ không thể tìm được một thừa số không tầm thường chia n mà không có phần dư.
Thuật toán O(n) để kiểm tra xem một số có phải là số nguyên tố trong Python không
Trong phần này, hãy chính thức hóa cách tiếp cận các hàm Python ở trên.
Bạn có thể đi qua tất cả các số từ 2 đến n- 1 sử dụng đối tượng range() trong Python.
Trong Python, phạm vi (bắt đầu, dừng, bước) trả về một đối tượng phạm vi. Sau đó, bạn có thể lặp lại đối tượng phạm vi để có được chuỗi từ đầu đến cuối theo các bước -1.
Bởi vì chúng ta cần một tập hợp các số nguyên từ 2 đến n-1chúng ta có thể chỉ định phạm vi (2n) và sử dụng nó cùng với vòng lặp for.
Đây là những gì chúng tôi muốn làm:
- Nếu bạn tìm thấy một số chia n không dư, bạn có thể nói ngay rằng số đó không phải là số nguyên tố.
- Nếu bạn lặp toàn bộ dãy số từ 2 lên đến n- 1 mà không tìm được số chia hết cho n thì số đó là số nguyên tố.
Hàm Python để kiểm tra số nguyên tố
Sử dụng cách trên, chúng ta có thể tự tin định nghĩa hàm is_prime() như sau.
def is_prime(n):
for i in range(2,n):
if (n%i) == 0:
return False
return TrueBây giờ chúng ta hãy phân tích định nghĩa hàm ở trên.
- Hàm is_prime() ở trên lấy một số nguyên dương n làm đối số.
- Nếu bạn tìm thấy một yếu tố trong một phạm vi nhất định (2N-1) thì hàm sẽ trả về Sai – vì số đó không phải là số nguyên tố.
- Và nó trả về True nếu bạn đi qua toàn bộ vòng lặp mà không tìm thấy thừa số.
Sau đó, hãy gọi hàm với các đối số và xác minh rằng đầu ra là chính xác.
is_prime(2) # True is_prime(8) # False is_prime(9) # False is_prime(11) # True
Qua kết quả trên có thể thấy 2 và 11 là số nguyên tố (hàm trả về giá trị True). VÀ 8 và 9 không phải là số nguyên tố (hàm trả về giá trị Sai).
Cách tối ưu hóa hàm is_prime() của Python
Ở đây chúng ta có thể làm một chút tối ưu hóa. Lưu ý danh sách các yếu tố trong bảng dưới đây.
số yếu tố61, 2, 36101, 2, 510181, 2, 3, 6, 918
Chà, chúng ta thấy rằng thừa số duy nhất của n lớn hơn n/2chỉ là n.
Điều này có nghĩa là bạn không cần phải lặp đến n 1. Thay vào đó, bạn chỉ có thể lặp tới n/2.
Nếu bạn không tìm thấy một yếu tố không tầm thường cho đến n/2bạn cũng không thể tìm thấy nó bên ngoài n/2.
Bây giờ, hãy sửa đổi hàm is_prime() để kiểm tra các thừa số trong phạm vi (2N/2)
def is_prime(n):
for i in range(2,int(n/2)):
if (n%i) == 0:
return False
return TrueHãy tiếp tục và xác minh đầu ra bằng một vài lời gọi hàm.
is_prime(9) # False is_prime(11) # True
Mặc dù có vẻ như chúng tôi đã tối ưu hóa nhưng thuật toán này không hiệu quả hơn thuật toán trước xét về độ phức tạp trong thời gian chạy. Trên thực tế, cả hai đều có độ phức tạp thời gian O(n): tỷ lệ thuận với giá trị của n hoặc tuyến tính theo n.
Chúng ta có thể làm tốt hơn không? Vâng, chúng tôi có thể!
▶️ Chuyển sang phần tiếp theo để xác định cách cải thiện độ phức tạp về thời gian của kiểm tra số nguyên tố.
Thuật toán O(√n) kiểm tra số nguyên tố trong Python
Nó xảy ra rằng các yếu tố của một số đi theo cặp.
Nếu a là một thừa số của n, thì cũng tồn tại một thừa số b sao cho axb = n, hay đơn giản là ab = n.
Hãy kiểm tra nó với một ví dụ.
Bảng dưới đây cho thấy các hệ số của số 18 theo cặp. Bạn có thể xác minh tương tự cho một vài số khác nếu muốn.
Cũng lưu ý rằng √18 xấp xỉ 424.
Và trong các thừa số xảy ra theo cặp (a, b), bạn có thể thấy rằng nếu a nhỏ hơn 4.24 thì b lớn hơn 4.24 – trong ví dụ này (218) và (3,6).
Thừa số của 18 theo cặp
Hình dưới đây cho thấy 18 hệ số được vẽ trên một trục số.
Nếu n trở thành một số chính phương, bạn sẽ có a = b = √n là một trong các thừa số.
▶️ Hãy xem 36 hệ số trong bảng dưới đây. Vì 36 là số chính phương nên a = b = 6 là một trong những yếu tố. Đối với tất cả các cặp yếu tố khác (a, b) a 6 Được hoàn thành.
Hệ số 36 theo cặp
Tóm lại, chúng ta có những điều sau đây:
- Mỗi số n có thể được viết là n = axb
- Nếu n là số chính phương thì a = b = √n.
- Và nếu a √n.
- Mặt khác, nếu a > b, thì a > √nib
Vì vậy, thay vì đi qua tất cả các số nguyên lên đến n/2, bạn có thể chọn một thiết bị lên đến √n. Và điều này hiệu quả hơn nhiều so với cách tiếp cận trước đây của chúng tôi.
Cách thay đổi thuật toán is_prime() thành O(√n)
Hãy chuyển sang phần tối ưu hàm kiểm tra số nguyên tố trong Python.
import math
def is_prime(n):
for i in range(2,int(math.sqrt(n))+1):
if (n%i) == 0:
return False
return TrueBây giờ hãy phân tích định nghĩa hàm ở trên:
- Để tính căn bậc hai của một số, hãy nhập mô-đun toán học tích hợp sẵn của Python và sử dụng hàm math.sqrt().
- Vì n có thể không phải là số chính phương nên chúng ta sẽ phải chuyển đổi nó thành một số nguyên. Sử dụng int(var) để truyền var thành int.
- Để đảm bảo rằng chúng tôi đang thực sự kiểm tra tới √n, chúng tôi thêm một dấu cộng vì phạm vi () loại trừ điểm cuối của phạm vi theo mặc định.
Ô mã bên dưới xác minh rằng hàm is_prime() của chúng ta đang hoạt động bình thường.
is_prime(8) # False is_prime(15) # False is_prime(23) # True
Trong phần tiếp theo, chúng ta hãy tạo một số đồ thị đơn giản để hiểu trực quan về O(n) và O(√n).
So sánh trực quan của O(n) và O(√n)
▶️ Chạy đoạn mã sau trong môi trường máy tính xách tay Jupyter mà bạn chọn.
import numpy as np
import seaborn as sns
import pandas as pd
n = 20
x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)
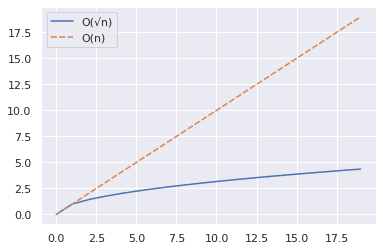
Đoạn mã trên cho thấy cách vẽ các đường cong cho ni √n cho một dải giá trị.
- Chúng tôi sử dụng hàm NumPy arange() để tạo một mảng số.
- Và sau đó, chúng tôi thu thập các giá trị ni √n tối đa nhưng không bao gồm 20, vào Khung dữ liệu gấu trúc.
- Sau đó, chúng tôi vẽ đồ thị bằng cách sử dụng hàm seaborn line graph().
Từ biểu đồ bên dưới, chúng ta thấy rằng √n nhỏ hơn nhiều so với n.
Bây giờ, hãy tăng phạm vi lên 2000 và lặp lại các bước tương tự như trên.
import numpy as np
import seaborn as sns
import pandas as pd
n = 2000
x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1,"O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)
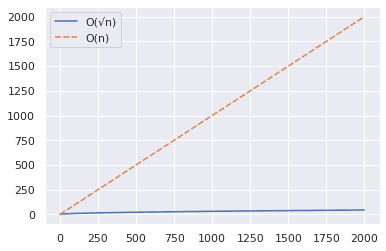
Từ biểu đồ trên, bạn có thể suy ra rằng thuật toán O(√n) nhanh hơn nhiều khi bạn kiểm tra một số lớn là số nguyên tố.
Đây là một ví dụ nhanh: 2377 là một số nguyên tố – hãy xem thử!😀
Mặc dù phương pháp O(n) sẽ thực hiện theo thứ tự 2000 bước, nhưng thuật toán O(√n) có thể giúp bạn nhận được câu trả lời chỉ sau 49 bước.✅
Đăng kí
⏳ Đã đến lúc tóm tắt nhanh.
- Để kiểm tra xem một số có phải là số nguyên tố hay không, một cách đơn giản là lặp qua tất cả các số trong phạm vi (2N-1). Nếu bạn không thể tìm thấy một thừa số chia n, thì n là số nguyên tố.
- Vì thừa số duy nhất n lớn hơn n/2 chỉ là n, bạn có thể chọn chỉ chạy tối đa n/2.
- Cả hai cách tiếp cận trên đều có độ phức tạp thời gian O(n).
- Vì các thừa số của số đi theo cặp nên bạn chỉ có thể chạy tới √n. Thuật toán này nhanh hơn nhiều so với O(n). Và mức tăng đáng chú ý khi kiểm tra xem một số lớn có phải là số nguyên tố hay không.
Tôi hy vọng bạn hiểu cách kiểm tra xem một số có phải là số nguyên tố trong Python hay không. Bước tiếp theo, bạn có thể xem hướng dẫn Python của chúng tôi về Thao tác chuỗi – nơi bạn sẽ tìm hiểu cách kiểm tra xem chuỗi có phải là palindromes, đảo chữ cái, v.v hay không.
Hẹn gặp lại bạn trong một hướng dẫn khác. Cho đến lúc đó, hãy tận hưởng việc viết mã!👩🏽💻
